| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- pytorch
- 대조학습
- pytorch forward 디버깅
- pytorch hook
- text embedding
- pytorch forward
- MCTS
- Python
- 스페인어학습지
- 스터디미니
- 강화학습
- 티스토리챌린지
- document layout analysis
- permutations
- 오블완
- 알파고
- 딥러닝
- Monte Carlo
- metric learning
- 환급기원
- 순열
- pytorch forward 연산
- MTBE
- TensorFlow
- 문서 파싱
- OCR
- AlphaGo
- document parsing
- 파이썬
- feature vector
- Today
- Total
Learn And Earn
몬테카를로 트리 탐색 - MCTS 본문
이번 포스팅에서는 Monte Carlo Tree Search 알고리즘에 대해서 알아보겠습니다. 이 알고리즘은 2016년, 알파고가 이세돌 선수에게 승리를 쟁취하는데에 기여한 알고리즘 중 하나입니다. 이 MCTS 알고리즘을 이용해서 이 player, 즉 알파고가 결정을 내려나갔다는 건데요, 기본적으로 바둑이라는 게임은 인공지능이 정복하기 어려운 게임 중 하나로 평가되는 게임이었습니다. 그럼에도 불구하고 승리를 가능케 한 MCTS 알고리즘은 어떠한 강점이 있기에 그런 어려운 문제를 풀어냈을까요? 먼저 스포일러를 하자면, "있음직한 게임의 경우의 수를 시뮬레이션을 통해 미리 헤아려보고, 그들을 토대로 하여 가장 합리적으로 보이는 수를 선택하는 것입니다.
어떤 문제를 해결해주는 알고리즘인가요?
Monte Carlo Tree Search는 기본적으로 경제학의 한 분야인 게임이론에서의 게임을 정복하기 위해서 고안된 알고리즘입니다. 여기서 말하는 게임은 오버워치, 메이플스토리 같은 일반적인 게임이 아닙니다. 기본적으로 경제학의 하위분야이기에 이 게임을 플레이하는 플레이어들은 각자가 서로의 이익을 극대화하기 위해 이기적으로 행동하고 있다고 가정하고 있습니다. 그리고 이러한 게임을 분류하는 기준이 여러가지가 있지만 저희는 딱 3가지 분류에만 집중해보겠습니다.
- Deterministic vs Stochastic
- 의미 : 말 그대로 각 플레이어가 현재 상황을(state) 고려하여 어떠한 결정을 내려 action을 취한다면, 그 결과로써 발생하는 다음 게임 state이 Deterministic하게 결정된다는 것입니다. 반대로 stochastic 게임이라면 state, action이 명시되어 있어도, 그 결과로 발생하는 새로운 상황은 randomness를 갖고 발생한다는 것입니다.
- 가장 쉬운 예시로는 부루마블에서의 주사위 던지기라는 걸 생각해보면 쉽겠죠? 이에 반해 주사위를 굴려 숫자가 realization이 진행되었다면 그에 따라 이동할 칸은 결정이 되는 건 또 deterministic하고요.
- Perfect Information vs Partially Observable
- 의미 : 나나 상대편이나 모두 같은 정보를 공유하고 있는 경우를 perfect information을 말합니다. 반대로 플레이어마다 관측하고 인지하고 있는 정보가 서로 다를경우를 Partially Observable이라고 하죠.
- 예시 : 원카드 같은 게임은 플레이어는 카드 뭉치에 어떤 카드가 있는지도 모르고 상대 패도 모르기 때문에 partially observable 게임입니다. 반대로 체스같은 경우는 플레이어가 자기가 따로 말을 숨겨뒀다가 몰래 놓으려 하지 않는 이상 모두 같은 게임 상황을 공유하고 있죠.
- Zerosum vs Non-zerosum
- 의미 : Zerosum은 상대와 내가 얻을 수 있는 이익의 합이 상수값으로 일정한 경우입니다. 반대로 non-zerosum은 zerosum이 아닌 게임을 일컫습니다.
- 예시 : 슈퍼마리오 메이커를 예시로 들어볼까요? 협동모드와 같은 경우, 다 같이 깃발을 잡고 승리를 이기는 것이 목표지만, 배틀모드의 경우 오직 한명만이 승자, 나머지는 패자로 분류됩니다. 그렇기에 전자는 제로썸, 후자는 논 제로썸이겠습니다.
- 추가 코멘트 - 앞으로의 논의에서 계속 중요하게 쓰일 성질입니다. 제로썸 게임을 나와 상대방이 하고 있다는 것은,
- 나의 이득의 증진은 곧 상대의 손해이고,
- 나의 이득의 감소는 곧 상대의 이득입니다.
- 즉, 상대편은 자기의 이득을 극대화하려 할텐데, 이는 제 이득을 최소화하려는 방향의 노력과 정확히 일치한다는 것입니다.
저희는 알파고의 자취를 따라가고 싶습니다. 그렇기에 바둑이 속하는 Deterministic, Perfect Information, Zerosum 게임에 집중을 해보겠습니다.
이전의 시도들
이러한 게임을 어떻게 하면 최대한 이득을 얻을 수 있을까요? 이 문제를 풀기 위한 알고리즘으로 가장 잘 알려진 알고리즘은 바로 minimax알고리즘입니다. minimax 알고리즘은 아래와 같이 recursive하게 정의됩니다.
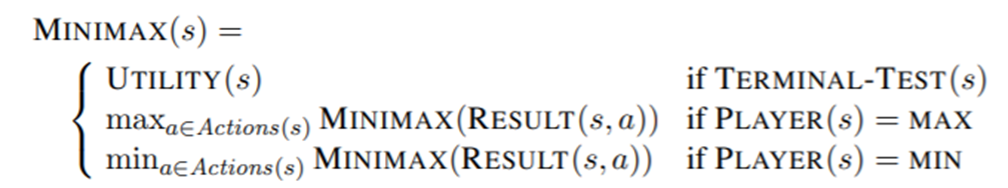
의미
아래의 아주 단순한 게임을 예시로 하여 설명을 해보겠습니다.

Leaf node에 적혀있는 숫자들은 utility입니다. 즉, 게임이 끝났을 때 발생하는 어떠한 스칼라 또는 벡터의 값인데요,
이 game tree의 경우 leaf node에는 플레이어 이름 MAX가 얻는 utility값이 적혀있습니다.
그럼 MAX 플레이어는 그럼 본인이 가질 수 있는 utility중 가장 큰 값은 14이니 action으로 a3를 선택하면 되겠네요 그쵸? 아닙니다.
제가 뭐라고 했죠? 여기서의 게임 플레이어들은 각자가 최대한으로 이기적이고 전략적으로 행동하고 있습니다. 그렇기 때문에 MAX가 a3를 선택한다고 해도 MIN플레이어가 14점 먹게 d1을 선택할리가 없죠. zerosum에서 설명했듯이, MIN플레이어는 MAX의 utility를 최소화하는 방향으로 행동할 것입니다. 그렇기 때문에 state D에서 action d3를 선택해 결과적으로 MAX 플레이어는 utility값 2를 얻게 되겠습니다.
그럼 이제 recursion fomula를 다시 한 번 살펴보겠습니다. MIN은 MAX의 utility를 최소화하려하고, MAX는 MAX의 utility를 최대화 하려 합니다. 그렇기 떄문에 각 플레이어의 상황에서 다음으로 발생할 수 있는 상황에 대한 utility값을 각각 최소화/최대화 하려는 것이지요. 그것을 수식으로 표현하면 위의 수식과 같습니다.
Minimax 알고리즘의 한계
여러분이 기억하셔야 할 것이 있습니다. root 노드에서의 함수를 한 번 호출했다고 해서, 함수의 호출이 한 번만 일어난게 아닙니다. 이러한 recursion function은 recursion tree, 여기서는 game tree의 각 노드에서 한 번씩 호출이 일어나는 것입니다. 그렇기때문에 시간복잡도가 game tree의 크기에 비례하죠. 위의 예시에서는 플레이어 각각이 한 턴씩만 진행하는 있을 것 같지도 않은 바보같은 게임을 예시로 들어 minimax로 해결을 할 수 있었지만, 보통의 경우 game tree는 매우 큽니다. 예를 들어 체스를 보겠습니다. 체스는 보통 한 수에 평균적으로 35가지의 수를 두는 가지수가 있다고 합니다. 그리고 한 게임은 평균적으로 각각 50수를 두고난 후 게임이 끝난다고 하네요. 즉 평균적으로 35^100, 대략 10^154 개의 노드가 있는 거네요. 그렇다는 것은 함수를 10^154번이나 호출한다는 것인데, 현실적으로 감당이 안됩니다.
요약하자면, Minimax 알고리즘은 gametree 전체를 입력받아 그들을 모두 훑어가며 최적의 수를 계산하는 것입니다.
정확히 말하자면 최적의 수를 두었을 때 얻을 수 있는 점수를 계산하는 것이죠.
계산비용을 절감하기 위해 어떤 수를 써야합니다. 위의 game tree 그림을 다시 살펴볼까요?
제가 설명했던 14점 예시를 다시 생각해봅시다. MIN플레이어가 바보가 아닌 이상 d3를 d1을 선택하지는 않겠죠?
이러한 바보같은 trajectory도 input으로 넣어 계산할 필요가 있을까요? 그렇지 않죠? 이와 같이 "있음직한, 즉 " partial tree를 활용하는 것이 바로 MCTS 알고리즘의 핵심 아이디어입니다.
이번 포스팅에서는 MCTS에 대해서 본격적으로 설명하기에 앞서, 어떠한 문제를 푸는 알고리즘이고, 어떠한 방법으로 이전에 풀려고 시도했는지를 살펴보았습니다. 다음 포스팅에서는 본격적으로 MCTS 알고리즘 안 쪽을 들여다 보겠습니다.
다음 포스팅에서 뵙겠습니다. 감사합니다.
'강화학습' 카테고리의 다른 글
| 강화학습 - tree policy 와 MCTS (0) | 2021.08.25 |
|---|---|
| 강화학습 - MDP (0) | 2021.07.03 |


